En este trabajo, estableceremos las propiedades dinámicas de modelos de depredación del tipo Leslie-Gower, en el que se incorpora una de estas formas, descrita por la función
![]() , con
, con
![]() .
.
La principal dificultad del análisis se debe a que esta función no es diferenciable para ![]() , y la matriz Jacobiana no está definida en los puntos de equilibrio sobre el eje horizontal (eje
, y la matriz Jacobiana no está definida en los puntos de equilibrio sobre el eje horizontal (eje ![]() ).
).
Previamente mostramos un resumen con las propiedades fundamentales del modelo del tipo Leslie-Gower, con el objeto de efectuar un adecuado análisis comparativo con modelos donde se incorpora la auto-interferencia entre los depredadores.
Para reforzar nuestros resultados se muestran algunas simulaciones numéricas.
![]()
In this work, we will establish the dynamical properties of the Leslie-Gower type predation model, in which is incorporated one of these form, described by the function
![]() , with
, with
![]() .
.
The main difficulty of the analysis is due to this function is not differentiable for ![]() , and the Jacobian matrix is not defined in the equilibrium points over the horizontal axis (
, and the Jacobian matrix is not defined in the equilibrium points over the horizontal axis (![]() ).
).
Previously, we showed a summary with the fundamental properties of the Leslie-Gower type model, in order to carry out an adequate comparative analysis with models where self-interference between predators is incorporated.
To reinforce our results, some numerical simulations are shown.
![]()
La relación dinámica entre los depredadores y sus presas ha sido y seguirá siendo uno de los temas dominantes en Ecologıa Teórica (Ecologıa Matemática) y particularmente en Dinámica Poblacional. Esto es debido a su existencia universal [8] y porque permite una mejor comprensión del comportamiento de las cadenas alimenticias o redes tróficas [30,38].
El primer modelo depredador-presa fue propuesto por el matemático italiano Vito Volterra [6,7] en una conocida monografıa publicada en 1926 [39], siendo descrito por un sistema no-lineal de Ecuaciones Diferenciales Ordinarias (EDO); este modelo coincidió con un modelo bidimensional para interacciones bioquımicas propuesto anteriormente por el matemático-fısico estadounidense Alfred J. Lotka: por esto el sistema de EDOS,es conocido con el nombre de modelo de Lotka-Volterra [7,30,31,38].
La caracterıstica principal de este primer modelo es que el único punto de equilibrio positivo para toda condición de parámetros es un centro [10,14], es decir, todas las trayectorias son órbitas cerradas concéntricas alrededor de ese punto. Esto implica que los tamaños poblacionales de los depredadores y sus presas oscilarıan permanentemente alrededor de ese punto para cualquier condición inicial [31]. Este comportamiento de las soluciones del sistema, fue bastante cuestionado porque en la naturaleza no se encuentran interacciones depredador-presa en que existan siempre comportamientos periódicos de los tamaños poblacionales de ambas especies, cualquiera sean las cantidades iniciales consideradas [30,38].
A partir del trabajo de Volterra, se sucedieron distintas propuestas para enfrentar y resolver las diversas objeciones formuladas [34]. Una de las primeras propuestas para solucionar algunas de las objeciones al modelo de Lotka-Volterra fue formulada por el biólogo ruso Georgii F. Gause (1910-1986), quien en 1934 [20] propuso un modelo que toma en cuenta la competencia intraespecıfica de las presas [20], reemplazando el crecimiento Malthusiano incorporado en el modelo de Lotka-Volterra, por la función de crecimiento logıstico (también llamada de ecuación de Verhulst-Pearl [6]).
Un resultado importante es el Teorema propuesto por el matemático ruso Andrei N. Kolmogorov en 1936 [7,30], que establece condiciones en el sistema bidimensional de ecuaciones diferenciales no-lineales, para asegurar la existencia de una única solución periódica estable [13] (matemáticamente, un ciclo lımite atractor). Para el fenómeno de oscilaciones de los tamaños poblacionales de presa y depredadores existe suficiente evidencia en la naturaleza [35] (llamados ciclos ecológicamente estables [13]).
Una alternativa diferente es el modelo propuesto por Patrick Holt Leslie en 1948 [28], que no se ajusta al esquema del modelo de Lotka-Volterra [38]. A diferencia de los modelos compartimentados del tipo Gause [16,38], basados en un principio de trasferencia de masa o energıa [8], el modelo de Leslie se caracteriza porque la ecuación de crecimiento de los depredadores es del tipo logıstico [6], considerando implıcitamente que existe competencia o auto-interferencia entre los depredadores
Leslie asumió que la capacidad de soporte del medio ambiente
convencional (environmental carrying capacity) ![]() es proporcional a la
abundancia de presas
es proporcional a la
abundancia de presas ![]() [30], esto es, se asume que
[30], esto es, se asume que
![]() ,
donde
,
donde ![]() representa el tamaño poblacional de las presas.
Este supuesto es también asumido en el modelo de Leslie derivado,
llamado modelo de May-Holling-Tanner [4,18,30,33,38].
representa el tamaño poblacional de las presas.
Este supuesto es también asumido en el modelo de Leslie derivado,
llamado modelo de May-Holling-Tanner [4,18,30,33,38].
Sin embargo, cuando el depredador es generalista y no existen presas
disponibles, los depredadores pueden cambiar a una fuente de alimento
diferente [3,25,37]. En este caso, la capacidad de soporte del medio ambiente de los
depredadores se puede expresar como ![]() , donde el parámetro
, donde el parámetro ![]() , indica la cantidad de alimento alternativo disponible para los
depredadores [37]. Obtenemos ası, un modelo de Leslie-Gower modificado [5].
, indica la cantidad de alimento alternativo disponible para los
depredadores [37]. Obtenemos ası, un modelo de Leslie-Gower modificado [5].
Por otra parte, la acción de los depredadores en la interacción se denomina respuesta funcional de los depredadores o función de consumo [16,30]; se refiere al cambio en la densidad de presa atacada por unidad de tiempo por depredador, cuando la densidad de presa cambia [16]. Se clasifican en varios tipos, dependiendo del tamaño de la población de presas o del tamaño de ambas poblaciones.
El Ecólogo canadiense Crawford S. Holling (1930-2019) en 1959 [26] describió tres tipos de funciones saturadas, basadas en experimentos realizados en laboratorio, las cuales consideró sólo dependientes del tamaño de la población de presas (conocidas como respuesta funcional presa-dependiente).
Posteriormente, Robert J. Taylor en 1984 [36] propuso la respuesta funcional no monotónica, usualmente usada para describir el fenómeno ecológico denominado formación de grupo de defensa [23,37]. Las respuestas funcionales presa-dependiente se nombran como respuestas funcionales del tipo Holling, I, II, IV [36] y existen diversas formas matemáticas para describirlas [30,38].
También han sido propuestas respuestas funcionales que son dependientes de ambas poblaciones tales como la de Beddington-DeAngelis [21,40], las razón-dependiente [38], etc.
En el modelo de Leslie [29], la respuesta funcional del depredador
es expresada por la función lineal ![]() , también usada en el
clásico modelo de Lotka-Volterra [30,38]. Sin embargo, esta
respuesta funcional no corresponde a ninguno de los tipos propuestos por
Holling [26], por no ser acotada.
, también usada en el
clásico modelo de Lotka-Volterra [30,38]. Sin embargo, esta
respuesta funcional no corresponde a ninguno de los tipos propuestos por
Holling [26], por no ser acotada.
En este trabajo estudiaremos el modelo de Leslie-Gower considerando el fenómeno denominado interferencia o competición entre los depredadores (CED), lo cual significa que dos o más depredadores (de la misma especie) se molestan al capturar las presas y por eso las presas pueden evitar la depredación [16].
Una situación similar se puede asumir en modelos Bioeconómicos de acceso abierto, cuando los pescadores se dirigen a un mismo lugar con sus botes o embarcaciones pesqueras para capturar un cardumen de peces; los botes pueden chocar entre ellos [11] e incluso originarse agresiones entre las tripulaciones (efectuando disparos, rotura de implementos de pesca, etc.), como ha sucedido en diversos lugares del planeta [11,12].
Existen tres formas para representar matemáticamente la CED, siendo una de ellas la respuesta funcional de Beddington-DeAngelis [21,38]. Asumiremos la expresión formulada por el matematico canadiense Herbert I. Freedman en 1979 [17], modificando el supuesto de los modelos habituales. Asumió un cambio en la función de depredación proponiendo la función [17]:
![]()
![]() , con
, con
![]() .
.
donde ![]() es la constante de interferencia mutua, y
es la constante de interferencia mutua, y
![]() es la respuesta funcional del depredador dependiente sólo de la población de presas.
es la respuesta funcional del depredador dependiente sólo de la población de presas.
En el siguiente gráfico vemos el comportamiento de la función
![]() , con
, con
![]() , para diferentes valores
de
, para diferentes valores
de ![]() .
.
Se observa que si ![]()
![]() , la gráfica de la función
crece en forma mas abrupta. Esto significa que la competición entre
los depredadores es más intensa, mientras que para valores grandes de
, la gráfica de la función
crece en forma mas abrupta. Esto significa que la competición entre
los depredadores es más intensa, mientras que para valores grandes de
![]()
![]() la competición va disminuyendo. Cuando
la competición va disminuyendo. Cuando
![]() , se tiene el modelo original de Leslie-Gower [29].
, se tiene el modelo original de Leslie-Gower [29].
Este trabajo está enfocado en el análisis de un modelo derivado del modelo de Leslie-Gower, asumiendo que los depredadores compiten entre ellos y no disponen de un alimento alternativo.
El resto del artıculo está organizado como sigue: En la Sección 2 haremos la formulación de los modelos en estudio y las propiedades básicas del modelo de Leslie-Gower. En la sección 3 mostraremos las propiedades principales del modelo asumiendo CED. En la Sección 4 presentaremos algunas simulaciones computacionales y en la Sección 5 discutiremos las consecuencias de la CED en el modelo del tipo Leslie-Gower modificado
En esta sección, presentaremos las propiedades fundamentales del modelo de Leslie (o de Leslie-Gower) propuesto en 1948 [28] y el modelo de Leslie-Gower modificado considerando alimento alternativo para los depredadores.
En adelante denotaremos por ![]() e
e ![]() los tamaños
poblacionales de presas y depredadores, respectivamente, medidos en número de individuos, biomasa o densidad por unidad de área o volumen, en
cualquier instante
los tamaños
poblacionales de presas y depredadores, respectivamente, medidos en número de individuos, biomasa o densidad por unidad de área o volumen, en
cualquier instante ![]() . Además,
. Además,
![]() e
e
![]() (No hay generación espontánea en el medio ambiente).
(No hay generación espontánea en el medio ambiente).
Es descrito por el sistema de ecuaciones diferenciales no lineales del tipo Kolmogorov [16,22]:
Los parámetros son todos positivos, esto es,
![]() , teniendo los siguientes significados ecológicos:
, teniendo los siguientes significados ecológicos:
![]()
![]() es la tasa intrınseca del crecimiento de las presas;
es la tasa intrınseca del crecimiento de las presas;
![]() es la capacidad de soporte del medio ambiente para las presas;
es la capacidad de soporte del medio ambiente para las presas;
![]() es la tasa máxima de consumo per capita, es decir, la máxima
cantidad de presas necesarias que pueden ser comidas por cada depredador en cada unidad de tiempo;
es la tasa máxima de consumo per capita, es decir, la máxima
cantidad de presas necesarias que pueden ser comidas por cada depredador en cada unidad de tiempo;
![]() es la tasa intrínsica del crecimiento de los depredadores;
es la tasa intrínsica del crecimiento de los depredadores;
![]() es la calidad de las presas como alimento para los depredadores.
es la calidad de las presas como alimento para los depredadores.
Las principales propiedades dinámicas del modelo de Leslie-Gower
descrito por el sistema (2.1) o campo vectorial
![]() son:
son:
![]()
Claramente, el sistema ![]() no está definido en
no está definido en ![]() , pero la isoclınica (isoclina) de los depredadores pasa por el punto
, pero la isoclınica (isoclina) de los depredadores pasa por el punto
![]() . Sin embargo estudiaremos su incidencia en la dinámica del sistema (2.1).
. Sin embargo estudiaremos su incidencia en la dinámica del sistema (2.1).
![]() ,
,
es una región positivamente invariante.
Se puede demostrar usando la compactificación de Poincaré [32] o usando desigualdades diferenciales [9].
Esta propiedad muestra que el modelo está bien formulado [8].
![]() ,
,
es también una región positivamente invariante.
Notamos que si ![]() , entonces,
, entonces,
![]() . Esto implica que
la población de depredadores va a la extinción.
. Esto implica que
la población de depredadores va a la extinción.
Si
![]() , la población de presas
crece.
, la población de presas
crece.
Si
![]() , la población de
presas se extingue.
, la población de
presas se extingue.
Por lo tanto
![]() , siempre existe en el interior
del primer cuadrante
, siempre existe en el interior
del primer cuadrante
![]() .
.
 .
.
Notamos que la matriz Jacobiana no está definida para ![]() .
.
La matriz Jacobiana evaluada en el punto
![]() es
es
 .
.
y det
![]() .
.
Luego, aplicando el Teorema de la traza y el determinante [15,31], se obtiene la tesis.
Aunque el modelo de Leslie-Gower no está definido en el punto
![]() , estudiaremos su influencia en la dinámica del
modelo. Mediante una reparametrización y un reescalamiento del tiempo
(variable independiente), estudiaremos un sistema topológicamente
equivalente.
, estudiaremos su influencia en la dinámica del
modelo. Mediante una reparametrización y un reescalamiento del tiempo
(variable independiente), estudiaremos un sistema topológicamente
equivalente.
Sean ![]() ,
, ![]() y
y ![]() . Después de un proceso algebraico se
obtiene el nuevo sistema
. Después de un proceso algebraico se
obtiene el nuevo sistema
donde
![]() , con
, con
![]() y
y
![]() . El sistema (2.2) o campo vectorial
. El sistema (2.2) o campo vectorial
![]() es una extensión continua del sistema (2.1).
es una extensión continua del sistema (2.1).
Los puntos de equilibrio son
![]() ,
,
![]() y
y
![]() con
con ![]() satisface la ecuación de la
isoclinas.
satisface la ecuación de la
isoclinas.
Obtenemos la ecuación polinomial
![]() , es decir,
, es decir,
![]() .
.
La matriz Jacobiana del sistema (2.2) es

Luego,

Para desingularizar el punto
![]() usaremos el método del
blowing-up direccional
usaremos el método del
blowing-up direccional
Sean ![]() y
y ![]() . Luego,
. Luego,
![]() ,
,
![]()
Reemplazando y factorizando se obtiene

Reescalando la variable independiente (el tiempo) por
![]() , se
obtiene
, se
obtiene
![]() ,
,
![]() .
.
Por lo tanto, se obtiene el sistema del tipo de Kolmogorov

La matriz Jacobiana del campo vectorial
![]() es
es

La matriz Jacobiana evaluada en
![]() es
es

Luego, el punto
![]() del campo vectorial
del campo vectorial
![]() es
es
| I) | una silla hiperbólica, si y sólo si, |
| II) | Un nodo repulsor, si y sólo si, |
| III) | Una silla-nodo repulsora, si y sólo si, |
Entonces, por el blowing-down, el punto de equilibrio no-hiperbólico
![]() del campo vectorial
del campo vectorial
![]() es una
silla-nodo repulsor para todo valor de
es una
silla-nodo repulsor para todo valor de ![]() .
.
Por tanto, el punto de equilibrio no-hiperbólico
![]() del campo vectorial
del campo vectorial
![]() es una silla-nodo repulsor
para todo valor de
es una silla-nodo repulsor
para todo valor de ![]() .
.
En consecuencia, el punto
![]() de la extensión continua
del modelo de Leslie-Gower tiene un comportamiento de silla-nodo repulsor
de la extensión continua
del modelo de Leslie-Gower tiene un comportamiento de silla-nodo repulsor
El sistema (2.2) se puede utilizar para demostrar todas las propiedades del sistema (2.1).
Por ejemplo, la matriz Jacobiana del campo vectorial
![]() o
sistema (2.2) evaluada en el punto de equilibrio
o
sistema (2.2) evaluada en el punto de equilibrio
![]() , equivalente al punto
, equivalente al punto
![]() del sistema (2.1), es
del sistema (2.1), es
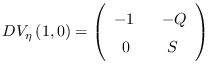
Luego, det
![]() , y el punto
, y el punto
![]() es una silla hiperbólica.
es una silla hiperbólica.
La matriz Jacobiana del campo vectorial
![]() topológicamente equivalente
topológicamente equivalente
![]() en el punto
en el punto
![]() es
es
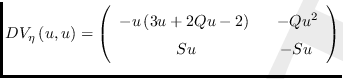 .
.
Luego,
det
![]() , y
, y
tr
![]() .
.
En el punto
![]() , se tiene
, se tiene
det
 , y
, y
tr
![]() .
.
Por tanto, el punto de equilibrio
![]() es un atractor local.
es un atractor local.
Considerando el Teorema de Poincaré-Bendixson válido sólo para
sistemas bidimensionales, se tiene que el punto de equilibrio
![]() es g.a.e.
es g.a.e.
En consecuencia
![]() es g.a.e., en el sistema (2.1).
es g.a.e., en el sistema (2.1).
Observamos que la matriz Jacobiana evaluada en el punto
![]() es
es
 ,
,
También la estabilidad global se puede probar usando la función de Lyapunov [22] descrita por
 ,
,
con ![]() , una constante adecuada [27].
, una constante adecuada [27].
Esta función es muy parecida a una de las propuestas por B-S. Goh en 1980 [22].
Se aplica el criterio de Bendixson-Dulac [11,22,32] usando la función
![]() en el sistema (2.2).
en el sistema (2.2).
Se denomina modelo de Leslie-Gower modificado o que se ajusta al esquema de Leslie a un modelo descrito por un sistema EDO generalizado
donde
![]() es la tasa de crecimiento per capita de las presas,
es la tasa de crecimiento per capita de las presas,
![]() es la respuesta funcional o tasa de consumo de los
depredadores, dependiente sólo de la población de presas (respuesta
funcional presa dependiente) o de ambas poblaciones,
es la respuesta funcional o tasa de consumo de los
depredadores, dependiente sólo de la población de presas (respuesta
funcional presa dependiente) o de ambas poblaciones,
![]() es la capacidad de soporte de los depredadores,
dependiente del tamaño poblacional de las presas, y
es la capacidad de soporte de los depredadores,
dependiente del tamaño poblacional de las presas, y
![]() es la tasa de crecimiento intrınseco de los depredadores.
es la tasa de crecimiento intrınseco de los depredadores.
A partir del sistema (2.3) se pueden generar diversos modelos considerando diversos fenómenos ecológicos [1,18,24,37]
En este sección presentaremos el modelo derivado del modelo de Leslie que será analizados en la siguiente sección.
El modelo a estudiar es descrito por el sistema autónomo bidimensional de ecuaciones diferenciales no lineales del tipo Kolmogorov [16,22]:
Hacemos presente que el sistema (3.1) no está definido en ![]() ,
es decir, su dominio es el conjunto
,
es decir, su dominio es el conjunto
![]()
Con el objeto de simplificar los cálculos seguimos la metodologıa desarrollada en [1,2,18,19,24]; efectuamos un cambio de variables y un reescalamiento del tiempo como se muestra en la siguiente proposición.
Reemplazando y factorizando en el sistema (3.1) tenemos:
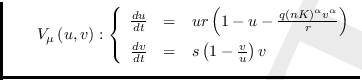
Este último sistema no está definido para ![]() .
.
Para subsanar esta dificultad, realizamos un reescalamiento del tiempo, dado
por
![]() .
.
Por regla de la cadena obtenemos
![]() y
y
![]()
Reemplazando en ell campo vectorial
![]() tenemos
tenemos
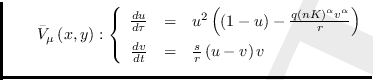
Definiendo
![]() y
y
![]() obtenemos el sistema (3.2).
obtenemos el sistema (3.2). ![]()
![]()
La matriz Jacobiana de la transformación ![]() es
es

y det
![]() .
.
Entonces, ![]() es un difeomorfismo que preserva la orientación del
tiempo, por lo cual el campo vectorial
es un difeomorfismo que preserva la orientación del
tiempo, por lo cual el campo vectorial ![]() es topológicamente
equivalente al campo vectorial
es topológicamente
equivalente al campo vectorial
![]() .
.
De esta forma, el sistema (3.2) es una extensión continua
del sistema (3.1), para ![]() , en particular en el punto
, en particular en el punto ![]() .
.
Puntos de equilibrio
Los puntos crıticos (estacionarios o de equilibrio) del sistema se
obtienen considerando
![]() , los cuales
corresponden a las soluciones de las ecuaciones:
, los cuales
corresponden a las soluciones de las ecuaciones:

De esta forma, los puntos de equilibrio sobre los ejes son ![]() ,
, ![]() y
y
![]() que satisface la ecuaciones de las isoclinas
(nulclinas)
que satisface la ecuaciones de las isoclinas
(nulclinas) ![]() y
y
 .
.

![]() .
.
Luego, ![]() es un cero (o raız) de la función
es un cero (o raız) de la función
![]() [19].
[19].
Observemos que
![]() es una función continua para todo
es una función continua para todo
![]() .
.
Como
![]() y
y ![]() entonces, por el Teorema del
Valor intermedio,
entonces, por el Teorema del
Valor intermedio,
![]() tiene un cero en el intervalo abierto
tiene un cero en el intervalo abierto
![]() .
.
Además, la derivada de ![]() con respecto a
con respecto a ![]() es
es
![]() para
para ![]() . Por lo tanto,
. Por lo tanto,
![]() es estrictamente creciente para todo
es estrictamente creciente para todo ![]() .
.
De esta forma, existe un único cero para la función ![]() para todo
para todo ![]() , y por consecuencia, existe un único punto de equilibrio positivo
, y por consecuencia, existe un único punto de equilibrio positivo
![]() para el sistema (3.2) al interior
del primer cuadrante.
para el sistema (3.2) al interior
del primer cuadrante. ![]()
Matriz Jacobiana
Para analizar la naturaleza de cada uno de los puntos de equilibrio, de acuerdo al Teorema de Hartman y Grossman (o Teorema de Linealización) [10,15], se debe analizar la matriz Jacobiana [4] (o matriz de la comunidad [38]) la cual es
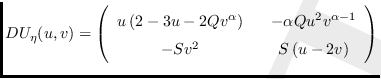
Notamos que
![]() no está definida para
no está definida para ![]() .
.
Para el sistema (3.2) tenemos las siguientes propiedades:

Considerando ![]() se tiene que
se tiene que
![]() y
cualquiera sea el signo de
y
cualquiera sea el signo de
![]() , las trayectorias con
condiciones iniciales en el plano de fase, fuera de la región
, las trayectorias con
condiciones iniciales en el plano de fase, fuera de la región
![]() entran en ella, mientras las que tienen condiciones iniciales
dentro de
entran en ella, mientras las que tienen condiciones iniciales
dentro de
![]() , permanecen allı
, permanecen allı
![]() .
.
Por lo tanto, se tiene que
![]() es una región de
invariancia para el sistema (3.2).
es una región de
invariancia para el sistema (3.2). ![]()
En la siguiente figura se muestra la región de invarianza
![]() .
.
![]()
Sean
![]() e
e
![]() , entonces,
, entonces,
![]()
![]()
Luego,
![]() y
y
![]() obteniendo
obteniendo
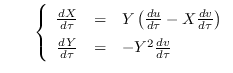
Luego, se tiene
![$\qquad U_{\eta }\left( X,Y\right) :\left\{
\begin{array}{rcl}
\frac{dX}{d\...
...\frac{X}{Y}-\frac{1}{Y}\right)
\frac{1}{Y}\right]%
\end{array}%
\right. $](img191.png)
Simplificando obtenemos
Este último sistema no está definido para ![]() Para solucionar
esta dificultad, se considera un reescalamiento del tiempo dado por
Para solucionar
esta dificultad, se considera un reescalamiento del tiempo dado por
![]() . Entonces, por regla de la cadena
. Entonces, por regla de la cadena
![]() y
y
![]() .
.
Aplicando estas relaciones al sistema
![]() se obtiene
se obtiene
![$\qquad \widetilde{U}_{\eta }\left( X,Y\right) :\left\{
\begin{array}{rcl}
...
...] \\
\frac{dY}{dT} & = & -SY^{2}\left( X-1\right)%
\end{array}%
\right. $](img198.png)

La matriz jacobiana del campo vectorial
![]() es
es

La cual no está definida para ![]() .
.
Aplicando el método de blowing up direccional, mediante el cambio de
variables
![]() entonces
entonces
![]() y
y
![]()
De esta forma, obtenemos el sistema

después de algunas manipulaciones algebraicas llegamos a
Hacemos un nuevo reescalamiento de la variable independiente (el tiempo)
dado por
![]() , entonces
, entonces
![]() y
y
![]() .
.
Aplicando estas relaciones al sistema (4.2) obtenemos
La matriz Jacobiana asociada al sistema del tipo
Kolmogorov (4.3) que es
 ,
,Luego,
 ,
,
Por consiguiente, el punto ![]() del campo vectorial
del campo vectorial
![]() es una silla hiperbólica. Luego es una silla
no-hiperbólica del campo vectorial
es una silla hiperbólica. Luego es una silla
no-hiperbólica del campo vectorial
![]() . Entonces, el punto
. Entonces, el punto
![]() es una silla
no-hiperbólica del campo vectorial compactificado de
es una silla
no-hiperbólica del campo vectorial compactificado de
![]() .
.
Por tanto, las trayectorias son acotadas. ![]()
La naturaleza de los puntos sobre los ejes no puede ser determinadas por los
métodos usuales en el sistema (3.2), porque la matriz Jacobiana no está
definida para ![]() .
.
Para el estudio de estos puntos haremos un nuevo cambio de variables en el sistema (3.2).
Sea
![]() , luego
, luego
![]()
Claramente si ![]() , entonces
, entonces ![]() . Además,
. Además,
![]() está definida para todo
está definida para todo
![]() .
.
Reemplazando tenemos que

o bien,
![]() .
.
Los puntos de equilibrio sobre los ejes son
![]() . Además, el
punto
. Además, el
punto
![]() debe satisfacer las ecuaciones de las
isoclinas (nulclinas),
debe satisfacer las ecuaciones de las
isoclinas (nulclinas),
![]() recta de pendiente negativa que
pasa por los puntos
recta de pendiente negativa que
pasa por los puntos
![]() y
y
![]() y,
y,
![]() , función creciente no acotada, por lo que se
puede asegurar la existencia de un punto de intersección
, función creciente no acotada, por lo que se
puede asegurar la existencia de un punto de intersección
![]() , con
, con ![]() .
.
La matriz Jacobiana es
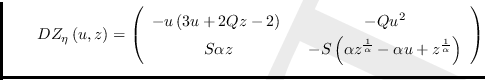 ,
,
definida para todo
![]() .
.
Para el sistema (4.4) tenemos las siguientes propiedades
![]()

Consideremos el blowing-up direccional [10,14] dado por
![]() y
y ![]() , donde
, donde ![]() y
y ![]() son funciones de
son funciones de ![]() . Se tiene
. Se tiene
![]() .
Luego,
.
Luego,
![]()
Reemplazando en el sistema
![]() se tiene el nuevo sistema
se tiene el nuevo sistema

factorizando obtenemos:

Reescalando el tiempo (variable independiente) ![]() , se tiene:
, se tiene:
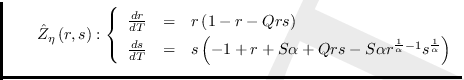
el cual es un sistema del tipo Kolmogorov y cuya matriz Jacobiana es:
 .
.
Evaluada en el punto
![]() se obtiene
se obtiene
 .
.
Luego,
![]() del campo vectorial
del campo vectorial
![]() es un punto:
es un punto:
i) repulsor hiperbólico, si y sólo si,
![]() ,
,
ii) silla-nodo hiperbólico, si y sólo si,
![]() , repulsor
por el
, repulsor
por el ![]() , y
, y
iii) silla-nodo no-hiperbólico, si y sólo si,
![]() ,
repulsor por el
,
repulsor por el ![]() .
.
Por lo tanto,
![]() del campo vectorial
del campo vectorial
![]() es silla-nodo no-hiperbólico repulsor, para todo
es silla-nodo no-hiperbólico repulsor, para todo ![]() y
y
![]() .
.
Por el blowing-down,
![]() del campo vectorial
del campo vectorial
![]() es silla-nodo no-hiperbólico repulsor, para todo
es silla-nodo no-hiperbólico repulsor, para todo
![]() .
. ![]()
![]()

Luego, el punto de equilibrio
![]() del sistema (4.4) o singularidad del campo vectorial
del sistema (4.4) o singularidad del campo vectorial
![]() es una silla hiperbólica para todo
es una silla hiperbólica para todo
![]() .
.
En consecuencia, el punto de equilibrio
![]() , del sistema (3.2) es una silla no-hiperbólica, para todo
, del sistema (3.2) es una silla no-hiperbólica, para todo
![]() .
. ![]()
Recordamos que el punto de equilbrio positivo,
![]() del campo vectorial
del campo vectorial
![]() o sistema (3.1) satisface las siguientes relaciones:
o sistema (3.1) satisface las siguientes relaciones:

![]()
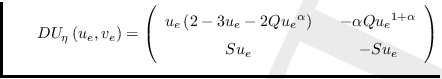
Finalmente, aplicando la relación
![]() , se
obtiene la matriz
, se
obtiene la matriz
 ,
,
obteniendo que
det
![]() , pues
, pues ![]() .
.
Por otra parte,
tr
![]() .
.
De esta forma,
![]() es local asintóticamente
estable.
es local asintóticamente
estable. ![]()
![]()

Definamos
![]() y
y
![]()
Entonces
![]()
Si ![]() entonces
entonces
![]() puesto que
puesto que
![]() para todo
para todo
![]() .
.
Si ![]() entonces
entonces
![]() y como
y como
![]() para todo
para todo
![]() .
.
Entonces,
![]() para todo
para todo
![]() .
.
Luego, por la linealidad de la integral
![]() .
.
Por lo tanto,
![]() para todo
para todo
![]() .
.
Notemos que
![]() es la función nula si y sólo si
es la función nula si y sólo si
![]()
De forma análoga ocurre con
![]() .
.
Si ![]() entonces
entonces
![]() puesto que
puesto que
![]() para todo
para todo
![]() .
.
Si ![]() entonces
entonces
![]() y como
y como
![]() entonces
entonces
![]()
Por lo tanto,
![]() para todo
para todo
![]() , y
, y
![]() es la función nula si y sólo si
es la función nula si y sólo si ![]() .
.
Ası,
![]() para todo
para todo
![]() y
y ![]() si y sólo si
si y sólo si
![]() .
.
Luego, ![]() es definida positiva en una vecindad perforada de
es definida positiva en una vecindad perforada de
![]() al interior del primer cuadrante.
al interior del primer cuadrante.
Por otra parte, la derivada de ![]() respecto al tiempo es
respecto al tiempo es

![]()
Usando las ecuaciones que satisface el punto de equilibrio
![]()
![]() y
y
![]()
tenemos que
![]()
![]()
![]()
![]()
Como
![]() , entonces existe un función
, entonces existe un función
![]() tal que
tal que
donde
![]() es una función de producto de potencias
de
es una función de producto de potencias
de ![]() y
y ![]() con coeficientes positivos.
con coeficientes positivos.
Luego,

Ası,
![]() para todo
para todo
![]() en el primer cuadrante.
en el primer cuadrante.
Ahora bien, como
![]() y
y
![]() .
.
![]()
![]()
Notemos que
![]() es una función positiva puesto que
es una función positiva puesto que
![]() y
y ![]() .
.
Luego, como cada sumando de
![]() es positivo, no existe
una raiz positiva de
es positivo, no existe
una raiz positiva de
![]() .
.
Por lo tanto, para ![]() tenemos
tenemos
![]()
Entonces, al interior del primer cuandrante,
![]() se anula si y sólo si
se anula si y sólo si
![]() .
.
Luego,
![]() es definida negativa en una
vecindad perforada de
es definida negativa en una
vecindad perforada de
![]() al interior del primer
cuadrante.
al interior del primer
cuadrante.
Finalmente, por el teorema de Lyapunov [32],
![]() es global asintóticamente estable (g.a.e).
es global asintóticamente estable (g.a.e). ![]()
![]()
Observemos que
![]() es continuamente diferenciable al
interior del primer cuadrante.
es continuamente diferenciable al
interior del primer cuadrante.
Ahora bien, considerando
![]()
con
![]() y
y
![]() , se tiene que:
, se tiene que:
![]()
![]()
![]() ,
,
para todo
![]() al interior del primer cuadrante.
al interior del primer cuadrante.
Por lo tanto, por el criterio de Bendixson-Dulac [10,32], no
existen ciclos al interior del primer cuadrante. ![]()
Para reforzar los resultados analıticos obtenidos para el sistema (3.2) se presentarán algunas simulaciones, indicando los valores de los parámetros utilizados.
En este trabajo se realizó el estudio de la dinámica de un modelo depredador presa del tipo Leslie-Gower considerando competencia (o interferencia) entre los depredadores CED, descrito por el sistema (3.1).
Hemos detallado también las principales propiedades del modelo de Leslie-Gower propuesto en 1948 [28,29] (sistema (2.1), con el objeto de efectuar un estudio comparativo sobre la influencia que tiene en el modelo original, la forma matemática de describir la CED.
Con el fin de simplificar los cálculos, se efectuó una reparametrización y un reescalamiento del tiempo se ha obtenido el sistema (3.2) topológicamente equivalente a (3.1).
Las principales caracterısticas del modelo de tipo Leslie-Gower modificado con CED son:
Por lo tanto, ambos modelos, con o sin CED, tienen la misma dinámica,
pues en ambos los puntos de equilibrio tienen las mismas caracterısticas (naturaleza), salvo la hiperbolicidad de los puntos de equilibrio
![]() en cada uno de los modelos.
en cada uno de los modelos.
Tanto en el sistema (3.1), como en el modelo de Leslie-Gower sin interferencia entre los depredadores descrito por el sistema (2.1), existe un único punto de coexistencia de las especies, que es atractor global asintóticamente estable (gae). Podemos afirmar entonces que ambos modelos son estructuralmente estables y además no existen bifurcaciones.
Esto significa que cualquiera sea el tamaño inicial de cada de las poblaciones, a medida que transcurra el tiempo, los tamaños poblacionales se estabilizan en dicho punto de equilibrio. Esta propiedad de ambos modelos es muy deseable por algunos ecólogos, o agencias que administran la explotación de recursos renovables.
Por ejemplo, si se considera que un cardumen de peces es capturado por
muchos interesados al mismo tiempo (pescadores artesanales o industriales, esto es, los seres humanos
actuando como depredadores [12]), la pesquerıa serıa sustentable.
Así se deduce en nuestro análisis, asumiendo la CED descrita por la función
![]()
![]() , con
, con
![]() .
.
Sin embargo, no podemos concluir que la CED induce la estabilidad de la interacción depredador-presa, pues sabemos que en muchas de las interaciones del mundo real, existen extinciones de una o ambas poblaciones [12], o bien oscilaciones periódicas de los tamaños poblacionales, las que pueden ser explicados por la existencia de ciclos límites [1,2,13] en el sistema dinámico que describe al modelo.
Estas diferentes situaciones son obtenidas como alternativas dinámicas posibles, en modelos que consideran la CED descrita por otras formas matemáticas. Tales casos se obtienen al asumir una respuesta funcional del tipo Beddington-DeAngelis [21] en el modelo de Leslie-Gower [40].
En este modelo, el punto de equilibrio positivo, no necesariamente es gae, cuando existe, y además existen ciclos lımites alrededor de un punto de equilibrio positivo, lo cual implica oscilaciones de los tamaños poblacionales [40]. Para un mismo conjunto de parámetros, coexisten comportamientos dinámicos distintos, debido a la aparición de curvas separatrices en el plano de fase [40]. Así, las trayectorias o soluciones del sistema son altamente sensibles a las condiciones iniciales.
De este modo surge la disyuntiva, sobre cual es el modelo más eficiente para representar una determinada interacción de depredación en la naturaleza. Nosotros creemos que una misma interacción puede ser representada por un modelo determinado (cualquiera sea su naturaleza matemática) en un momento o tiempo definido, pero su validez dependerá fuertemente de las hipótesis subyacentes, que usualmente no son declaradas.
Teniendo presente que la compledjidad dinámica de un sistema de EDO, no implica la complejidad ecológica del modelo descrito por ese sistema, no podríamos afirmar fehacientemente, que un modelo es mejor que otro. Sin embargo, situaciones ecológicas más complejas (por ejemplo considerar tiempo de gestación, distribución no-homogénea de las poblaciones o clasificados por edades y sexo, etc.) exigen el empleo de herramientas matemáticas más sofisticadas que las EDO.
![[*]](footnote.png)
![[*]](footnote.png)