Journal homepage    http://revistas.unitru.edu.pe/index.php/SSMM

Mathematical modeling of injury healing process under the action of an active pharmaceutical ingredient (API).


Modelamiento matemático del proceso de sanación de heridas bajo la acción de un ingrediente farmacéuticamente activo (IFA).

Alfredo Palomino I.

Leighton Estrada R.

Javier Valeriano M.

Sergio Luque M.

Received, Jul. 21, 2019 , Accepted, Set. 24, 2019 -

How to cite this article:
Palomino, A. et al. Mathematical modeling of injury healing process under the action of an active pharmaceutical ingredient (API). Selecciones Matemáticas. 2019; 6(2):283-288. http://dx.doi.org/10.17268/sel.mat.2019.02.14

Abstract

In this work we carried out the mathematical modeling of the wound healing process, which is a well documented topic in medical and biological practice; but mathematically speaking there are still too much to be done for a clear understanding of the healing phenomom. Here we contribute to the mathematical modelling by using chemical kinetic concepts and mathematical tools, from which we have been able to formulate a system of ordinary differential equations of initial value, whose solution is presented graphically in front of a case study, where we have tested an active pharmaceutical principle with respect to its effectiveness. Finally, the speed of the healing process for such a case study produced an excellent agreement with experimental data that has been omitted due to confidentiality.

Keywords. Injury, healing, mathematical modelling, pharmaceutically active principle, mechanism.

Resumen

En este trabajo llevamos a cabo el modelado matemático del proceso de curación de heridas, que es un tema bien documentado en la práctica médica y biológica; pero matemáticamente hablando, todavía hay mucho por hacer para una comprensión clara del fenómeno curativo. Aquí contribuimos al modelado matemático mediante el uso de conceptos de cinética química y herramientas matemáticas, a partir de los cuales hemos podido formular un sistema de ecuaciones diferenciales ordinarias de valor inicial, cuya solución se presenta gráficamente frente a un estudio de caso, donde hemos probado un principio farmacéuticamente activo con respecto a su eficacia. Finalmente, la velocidad del proceso de curación para tal estudio de caso produjo un excelente acuerdo con los datos experimentales, que se han omitido debido a la confidencialidad.

Palabras clave. Herida, curación, modelamiento matemático, principio farmacéuticamente active, mecanismo.

Introduction

The process of wound healing is a well documented issue in the medical and biological fields [5,13,3,1]. With respect to the mathematical field, despite the efforts of the last decade towards the mathematical understanding and modeling of this field, there is still much to do. From the review of the literature, we can report some interesting works related to mathematical modeling [3,7,4,6], which have been used as a framework to address our study. From the review of the literature on the process of wound healing, the four stages related to the healing process became clear [12]. These stages were used to postulate the occurrence of a pseudo molecular mechanism during the healing process, which was a key point for the formulation of the mathematical model. In addition, the formulated model was solved assuming some initial values ​​for the variables. The solution was carried out using Matlab and the results were presented graphically, matching appropriately for the case study of an active pharmaceutical ingredient [10,11].

Basic concept on the injury healing process

Before continuing with the application of the woung healing product, let us briefly look at the stages of wound healing, where most medical doctors agree in considering the following stages in a normal lineal healing process [12,2,8,9], these being:

1. Hemostasis , which consists of clothing the injury through the rapid formation of platelets, thrombi and fibrin.
2. Inflammation, consisting of swelling of the injured area as a defense against environmental aggression and pathogens.
3. Proliferation is the stage where the collagen granules are formed, leading to the formation of the capillaries and oriented fibers.
4. Consolidation is the last stage of the biochemical process of wound healing, where the wound is finally sealed and restored.

A pharmaceutical mixture and its enhanced potency for healing injuries

We should state beforehand that we are not aimed at accomplishing a whole protocol for a formal validation of a pharmaceutical formulation, but just to communicate an interesting finding concerning a product isolated and purified from an indigenous Peruvian plant.

Thus, the case study presented here involves the formulation of a product after choosing and isolating seven species out of the 37 identified by GC-MS analysis. These species represent the active pharmaceutical ingredient (API). These ingredients will be called A, B, C, D, E, F, G for reasons of confidentiality. These compounds are mixed with an excipient in a suitable proportion, also kept as a secrecy.

Injury treating procedure

Clean the injured area with distilled water and neatly pour the healing agent directly on the lesion. What follows is the immediate stop of bleeding and the formation of blood clots that then form a kind of seal of dry clots on the surface of the lesion. Subsequently, the surrounding area of the lesion is also covered with the IH-agent. From that moment on, the operation to cover the surrounding area is repeated every 6 hours until 5 or 6 days when the external dry cloth is dropped. Then, the IJ agent is used every 12 hours until the injury has been completely overcome.

Apparent molecular mechanism to approach the rate of the injury healing process

Despite the complexity of the biochemical process of healing, we are aimed at approaching the process from a rather simplified stand point of view, thus we postulate the idea of an intensive and highly dynamic interaction between the injured surface (both dermis and epidermis) and the active principles of the product formulated. Further we consider that the product may have a bio catalytic effect and gets absorbed easily by the cells therefore it facilitates the speed of healing process.

Assumptions

Lets state some fundamental assumptions:

1. The injured patient is a healthy person, whether young or old.
2. The injury does not compromise any vital organ of the injured person.
3. There is a strong electrostatic attraction between the injured area and the active ingredients of the formulated product.
4. The active principles interact with the injured surface cooperatively, so that some of them are prophylactic, others have antiseptic properties and some others are simply vectored carriers of the true active ingredients.
5. The bio active principles contained in the product catalyze the generation of granules to heal the injury.
6. In addition, the active principles promote the generation of connectives for the formation of capillaries and specialized cells.
7. Through some biochemical mechanism the active principles of the product are integrated to the cellular structure during the cell restoration without generating any secondary effects.
8. The active principles of the product act as smart molecules and prevent the formation of abnormal keloids post healing.
9. The injured surface versus healing product resembles a bi molecular solid-liquid heterogeneous reaction, whose apparent stoichiometry may be approached by a by molecular scheme, That is: $A_2+B_2 \rightarrow C$.
10. Despite the assumption $(9)$ is true, once the process begins, it switches instantaneously into a pseudo homogenous behavior at the gel interphase in order to facilitate the interaction among the cells concerned in the healing process.

Pseudo molecular mechanism to approach the understanding of the healing process

Following the statement delivered above, we propose the following pseudo molecular mechanism.

$$A_2 \xrightarrow{\hspace{0.5cm}{k_1}\hspace{0.5cm}} 2A^* hemostasis$$

$$B_2 \xrightarrow{\hspace{0.5cm}{k_2}\hspace{0.5cm}} 2B^* activation$$

$$A^* + B^* \xrightarrow{\hspace{0.5cm}{k_3}\hspace{0.5cm}} AB^* inflammation$$

$$AB^* + B^* \xrightarrow{\hspace{0.5cm}{k_4}\hspace{0.5cm}} ABB^* proliferation$$

$$ABB^* + B^* \xrightarrow{\hspace{0.5cm}{k_5}\hspace{0.5cm}} ABBB^* proliferation$$

$$ABBB^* + B^* \xrightarrow{\hspace{0.5cm}{k_6}\hspace{0.5cm}} C maturation$$

Where:

$$A_2 : \textit{\normalfont potential activity of injured area}$$

$$B_2 : \textit{\normalfont potential activity of the healing product}$$

$$A^* : \textit{\normalfont activity of injured area}$$

$$B^* : \textit{\normalfont activity of the healing product }$$

$$AB^* : \textit{\normalfont activated interaction during inflammation stage }$$

$$ABB^* : \textit{\normalfont activated interaction during proliferation stage }$$

$$ABBB^* : \textit{\normalfont activated interaction during maturation stage }$$

$$C : \textit{\normalfont restored tissue}$$

Formulation of the model

Applying molecular reaction consideration to the above-described mechanism, we have:

$$2 \frac{d[A^*]}{dt} = \frac{d[A_2]}{dt}$$

The rate equations for the process of injury healing may be stated as follows.

$$\frac{d[A^*]}{dt} = 2k_1[A_2] - k_3[A^*][B^*]$$

$$\frac{d[B^*]}{dt} = 2k_2[B_2] - k_3[A^*][B^*] -k_4[AB^*][B^*] - k_5[ABB^*][B^*]$$

$$\frac{d[AB^*]}{dt} = k_3[A^*][B^*] - k_4[AB^*][B^*]$$

$$\frac{d[ABB^*]}{dt} = k_4[AB^*][B^*] - k_5[ABB^*][B^*]$$

$$\frac{d[ABBB^*]}{dt} = k_5[ABB^*][B^*] - k_6[AB^*][ABBB^*]$$

Assuming that the injured tissue and the molecules of the healing product behave as reacting molecules, we may apply the Transition State Theory to the healing process overall. Then the differential equations converts into algebraic. In fact we may solve them applying conventional elimination method. Thus, we end up with the following relationship in order to account for the rate of healing.

$$\frac{d[A_2]}{dt} = \left(\frac{1}{k_5+k_6}\right)(k_1k_6[A_2] - k_2k_5[B_2])$$

In a simplified form:

$$\frac{d[A_2]}{dt} = K_1[A_2] - K_2[B_2]$$

Simulation procedure

The series of six differential equations of initial conditions derived in order to account for the injury healing process, have been solved using Matlab assuming some apparent values for the initial conditions as well as for the values of the kinetic constants for the healing process.

Numerical solution:

The numerical solution is carried out in Matlab.

Changing variables:

$$[A^*] = y_1$$

$$[B^*] = y_2$$

$$[AB^*] = y_3$$

$$[ABB^*] = y_4$$

$$[ABBB^*] = y_5$$

$$[A_2] = y_6$$

$$[B_2] = y_7$$

The system of non linear equations are:

$$\frac{dy_1}{dt} = 2k_1y_6 - k_3y_1y_2$$

$$\frac{dy_2}{dt} = \frac{2k_1}{k_5}(4k_5 + 5k_6)y_6 - \frac{k_3}{k_5}(5k_5 + 4k_6)y_1y_2 - k_4y_3y_2 - k_5y_4y_2$$

$$\frac{dy_3}{dt} = k_3y_1y_2 - k_4y_2y_3$$

$$\frac{dy_4}{dt} = k_4y_2y_3 - k_5y_2y_4$$

$$\frac{dy_5}{dt} = k_5y_2y_4 - k_6y_5$$

$$\frac{dy_6}{dt} = -4k_1y_6 + 2k_3y_1y_2$$

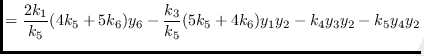The assumed initial conditions are:

$$y_1(0) = y_{10} = 1$$

$$y_2(0) = y_{20} = 1$$

$$y_3(0) = y_{30} = 0$$

$$y_4(0) = y_{40} = 0$$

$$y_5(0) = y_{50} = 0$$

$$y_6(0) = y_{60} = 1$$

The parameters are:

$$k_1 = 0.1$$

$$k_2 = 0.1$$

$$k_3 = 0.1$$

$$k_4 = 0.1$$

$$k_5 = 0.1$$

$$k_6 = 0.1$$

Time interval $=[0,120]$

The solution of the system of initial value ordinary differential equations are carried out in Matlab and the result is presented graphically inf Fig. 1.

Figura 5.1: Numerical solution of the injury healing process.

Figura 5.2: Phase diagram.

Empirical experience

Here we will show a Case Study, where the patient got an accidental injury after falling down and heating his forehead on an iron devise which was part of the central heating device put in a wrong place. The accident happened at around 3 AM. and he was alone experiencing a home accident which is related here. At that very moment, desperate because of the hemorrhage, the patient used the above-mentioned product, since he had no other appropriate product at hands.

Some comments on the model of healing rate of injuries

The mathematical model found applying simplifying assumptions stated earlier, sheds some light to the understanding of the rate of the healing process, which appears to be highly influenced by the activity and size of the injury itself as well as the activity of the healing agent. In fact, we may appreciate that injury and the injury-healing agent go in opposite directions, which sounds logical to start with.

On the other hand, even though we need to treat and to document many more cases for a right statistical validation on the effectiveness of the product, the unquestionable evidence of the photographical evidence stands alone speaking for itself that this is an unprecedented finding.

Discusion of results

The clear message of the simulated injury healing process is the fact that both, the ISA activity $$(y_6)$$ and the activity of the API $$(y_7)$$ are the key factors concerning the injury healing process. In fact both profiles describe sigmoidal shape going up to a final stage where the healing process gets consolidated.

Another important detail is that the intermediate stages describe a waved profile going downwards at the intial stage.

Concluding remarks

1. In this work we have been able to formulate the mathematical model for the injury healing process based on some simplifying assumptions concerning the four stages in which the healing process have been divided by the specialists, that is to say physicians.

2. The mathematical model has been simulated with Mathlab packeage and the apparent profiles of the healing process stages are shown in this contribution by first time.

3. The kinetic model generated under the simplifying assumption stated in this work, would be helpful for further studies on this subject, after implementing an appropriate experimental design for data collection.

4. The model formulated in this work to account for the injury healing process looks adequate and is the first step to go into more deeper analysis in future Works.

5. The simulation described above indicates the correctness of the model formulated in this study.

ORCID and License

Alfredo Palomino Infante https://orcid.org/0000-0002-6453-586X,

Leighton Estrada Rayme https://orcid.org/0000-0002-7858-5104,

Javier Valeriano Mamani https://orcid.org/0000-0003-0733-5906,

Sergio Luque Mamani https://orcid.org/0000-0001-6133-7748.

This work is licensed under the Creative Commons Attribution-NoComercial-ShareAlike 4.0.

Bibliografía

1

A. C. de O. G. et Al., Wound healing: Literature Review. 1995; 43(3):221–223.

2

Dokoumetzidis, A. and Macheras, P. A century of dissolution research: From Noyes and Whitney to the Biopharmaceutics Classification System. Int. J. Pharm. 2006; 321(1–2):1–11.

3

Eming, S. A., Martin, P. and Tomic-Canic, M. Wound Repair and Regeneration Mechanisms. Sci. TransL Med, 2014; 322(265):265sr6.

4

Flegg,J. A., Menon, S. N., Maini, P. K. and McElwain, D. L. S. On the mathematical modeling of wound healing angiogenesis in skin as a reaction-transport process Front. Physiol. 2015; 6(SEP):1–17.

5

Flynn, B. M. E. and Rovee,D. T. Healing Mechanisms. 2015; 82(10):1544–1549.

6

Geris, L., Gerisch, A., and Schugart, R. C. Mathematical Modeling in Wound Healing, Bone Regeneration and Tissue Engineering. Acta Biotheor., 2010; 58(4):355–367.

7

Kratz, G. Modeling of wound healing processes in human skin using tissue culture Microsc. Res. Tech. 1998; 42(5):345–350.

8

Leitão, F., Leitão, S. G., da Fonseca-Kruel, V. S., Silva, I. M. and Martins, K. Medicinal plants traded in the open-air markets in the State of Rio de Janeiro, Brazil: An overview on their botanical diversity and toxicological potential. Brazilian J. Pharmacogn. 2014; 24(2):225–247.

9

Madhumathi, K. et al., Development of novel chitin/nanosilver composite scaffolds for wound dressing applications. J. Mater. Sci. Mater. Med. 2010; 21(2):807–813.

10

Palomino-Infante, A. R. Modelling the dynamics of the pulsed isolation of essential oils. in IX Americas Conference on Diferential Equations, 2012; 30–35.

11

Palomino-Infante, A. R. Pulsed Isolation of Essential Oils Using Pulsed Steam. Ph.D. Thesis, FQIQ, UNMSM. 2016.

12

Peppas, N. A. and Langer, R. Origins and development of biomedical engineering within chemical engineering. Biomed. Res., 2004; 50:536–546.

13

Zhang,N., Yan, H. and Wen, X. Tissue-engineering approaches for axonal guidance. Brain Res. Rev., 2005; 49(1):48–64.

Notas al pie

... I.

Faculatad de Química e Ingeniería Química. Universidad Nacional Mayor de San Marcos, Perú (rpalominoi@unmsm.edu.pe).

... R.

Universidad Nacional Mayor de San Marcos, Perú. (lestrada@nexialinstitute.org),

... M.

Universidad Nacional Mayor de San Marcos, Perú. (jvaleriano@nexialinstitute.org),

... M.

Universidad Nacional Mayor de San Marcos, Perú. (sluque@nexialinstitute.org),