Siguiente: Extensión de la Desigualdad Subir: Una Extensión de la Anterior: Los Espacios BMO. Desigualdad
Sea
![]() una función positiva, no-decreciente, definida sobre
una función positiva, no-decreciente, definida sobre ![]() . Por definición,
. Por definición,
![$BMO_{\varphi} = \left\lbrace f \in L^{1}(Q_{o})/ \left[ f \right] _{BMO_{\varph...
...}\displaystyle\int_{Q} \vert f(x)-C_{Q}\vert dx \leq M < \infty \right \rbrace $](img36.png)
donde los cubos son asumidos de medida finita y lados paralelos a los ejes coordenados. Podemos usar ![]() en vez de la constante
en vez de la constante ![]() . Estos espacios
. Estos espacios
![]() fueron inicialmente considerados por S. Spanne en 1965. (Ver [4]). Se verifica que formas particulares de
fueron inicialmente considerados por S. Spanne en 1965. (Ver [4]). Se verifica que formas particulares de ![]() hacen coincidir isomorficamente
hacen coincidir isomorficamente
![]() con algunos clásicos espacios de funciones. Veamos,
con algunos clásicos espacios de funciones. Veamos,
![]() si
si
![]() ,
,
![]()
![]() ;
;
![]() si
si
![]() ,
,
![]() , entonces
, entonces
![]() , donde
, donde
![]() es el espacio de Lipschitz
es el espacio de Lipschitz
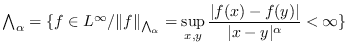 ;
;
Si
![]() , entonces
, entonces
![]() , con
, con
![]() , donde
, donde
![]() es el espacio de Morrey
es el espacio de Morrey
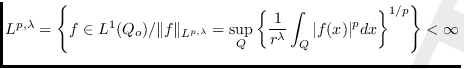 ,
,
donde ![]() es la longitud del lado de
es la longitud del lado de ![]() ,
,
![]() .
.
Si
![]() , entonces
, entonces
![]() .
.