Siguiente: The Tangent Vector Field Subir: Transversal Intersection Curves of Anterior: Darboux Frame of Null
The intersection curve of two spacelike surfaces is a spacelike, the intersection curve of two timelike surfaces may be spacelike or timelike, the intersection curve of two lightlike surfaces may be spacelike or null, the intersection curve of spacelike and timelike surfaces is spacelike, the intersection curve of spacelike and lightlike surfaces is spacelike, and the intersection curve of timelike and lightlike surfaces spacelike or null. We obtain the transversal intersection case, when the normal vectors of the surfaces are linearly independent.
For what follows we suppose
![]() be a transversal intersection curve of two
arbitrary surfaces
be a transversal intersection curve of two
arbitrary surfaces
![]() and
and
![]() and assume that the
curve
and assume that the
curve
![]() is a regular curve
parametrized by a parameter
is a regular curve
parametrized by a parameter ![]() with the same trace as the curve
with the same trace as the curve
![]() . Let
. Let
![]() and
and
![]() denote the
normal vector fields of the surfaces
denote the
normal vector fields of the surfaces ![]() and
and ![]() respectively. Also,
let
respectively. Also,
let
![]() and
and
![]() denote the unit normal vector
fields of the surfaces
denote the unit normal vector
fields of the surfaces ![]() and
and ![]() respectively. Assume that
respectively. Assume that
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() .
.
Since
![]() is orthogonal to
is orthogonal to
![]() and
and
![]() so by using proposition 2, we obtain
so by using proposition 2, we obtain
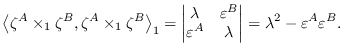 |