La distribución de Erlang es un caso particular de la distribución gamma y ocurre cuando se considera
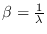 y
y
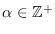 en su función densidad.
en su función densidad.
Es decir, la función densidad de la distribución Erlang con 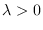 y
y
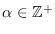 esta dado por
esta dado por
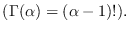
La media y la varianza de la distribución de Erlang son
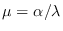
y
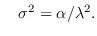
Inicialmente tuvo aplicación en la ingeniería de tráfico. Actualmente la distribución de Erlang tiene aplicación en el área de procesos estocásticos y en modelos de servicio masivo. Existe una asociación entre los modelos de probabilidad de Poisson y de Erlang.
Si el número de eventos aleatorios independientes que ocurren en un lapso específico es una variable aleatoria de Poisson con frecuencia constante igual 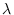 entonces para un
entonces para un 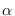 dado el tiempo de espera hasta que ocurra el
dado el tiempo de espera hasta que ocurra el 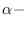 ésimo evento de Poisson sigue una distribución de Erlang.
El lector interesado en ver aplicaciones en la ingeniería de confiabilidad sugerimos ver [12].
ésimo evento de Poisson sigue una distribución de Erlang.
El lector interesado en ver aplicaciones en la ingeniería de confiabilidad sugerimos ver [12].
![]() y
y
![]() esta dado por
esta dado por
