From the results obtained in this work we can make the following conclusions:
Study the planar curvature lines of a hypersurface
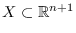 satisfying the conditions of Theorem 3.1 corresponds to study the Laplace invariants
satisfying the conditions of Theorem 3.1 corresponds to study the Laplace invariants
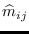 of the Gauss map, which in this case must be identically zero. All isothermic surface with respect to the third fundamental form satisfying the conditions of Theorem 2.2, with
two planar curvature lines can be written in terms of a holomorphic function and two real functions of one variable.
From a planar regular curve and its unit normal vector we can obtain a class of surfaces with one family of planar curvature lines and we can generalize these results to obtain classes of hypersurfaces with families of
of the Gauss map, which in this case must be identically zero. All isothermic surface with respect to the third fundamental form satisfying the conditions of Theorem 2.2, with
two planar curvature lines can be written in terms of a holomorphic function and two real functions of one variable.
From a planar regular curve and its unit normal vector we can obtain a class of surfaces with one family of planar curvature lines and we can generalize these results to obtain classes of hypersurfaces with families of 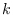 planar curvature lines.
Finally, this work can be used to classify hypersurfaces with planar curvature lines that satisfy an additional geometric or analytical property with prescribed Gauss map, future works in this direction we will be presenting.
planar curvature lines.
Finally, this work can be used to classify hypersurfaces with planar curvature lines that satisfy an additional geometric or analytical property with prescribed Gauss map, future works in this direction we will be presenting.