Example
In this section we consider an example where some
classical results cannot be
applied. However, we can apply
the Theorem 3.6.
Indeed, consider the differential equation
![$\displaystyle y^{(\mathrm{ iv})}-5y''+[\sin(t^q)+4]y=0,$](img94.png) ![$\displaystyle \mbox{with $q\in]2,\infty[$,}$](img95.png) |
|
|
(12) |
which is of type (1.1) with
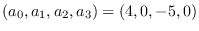 and
and
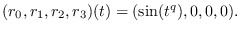 Then, the classical generalizations of Poincaré type theorems [26],
the Levinson Theorem [9, Theorem 1.3.1],
the Hartman-Wintner [9, Theorem 1.5.1]
or
the Eastham Theorem [9, Theorem 1.6.1]
can not be applied to obtain the asymptotic behavior of
(5.1).
However, the hypotheses of Theorem 3.6
are satisfied see [7].
Then, the asymptotic formulas are given by
Then, the classical generalizations of Poincaré type theorems [26],
the Levinson Theorem [9, Theorem 1.3.1],
the Hartman-Wintner [9, Theorem 1.5.1]
or
the Eastham Theorem [9, Theorem 1.6.1]
can not be applied to obtain the asymptotic behavior of
(5.1).
However, the hypotheses of Theorem 3.6
are satisfied see [7].
Then, the asymptotic formulas are given by
where
and 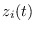 satisfies the following asymptotic behavior
satisfies the following asymptotic behavior
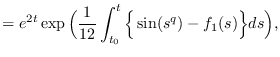
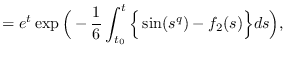
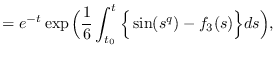
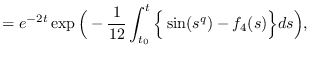
![\begin{align*}z_{i}(t),z'_{i}(t),z''_{i}(t)
=
\left\{
\begin{array}{lll}
\displa...
...(s^p)\vert ds\Big),
&
& i=4,\quad \beta\in ]0,1].
\end{array}\right.\end{align*}](img115.png)