Interpretación geométrica

Dado el problema programación lineal en su forma estándar

$$Minimizar\;\; c^Tx$$

$$sujeto\; a \;\; Ax=b$$ (1)

$$x\geq 0$$

donde $x\in{\mathbb{R}}^n$, $c\in{\mathbb{R}}^n$, $b\in{\mathbb{R}}^m$, $A\in{\mathbb{R}}^{m\times n}$, $ran(A)=m$.

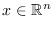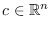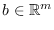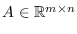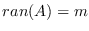Figura: Aproximación interior y búsqueda por la frontera a la solución óptima.

Una forma de resolver el problema (1.1) es usando el método simplex de programación lineal, que busca la solución óptima sobre la frontera de la región factible

$${\mathcal F}=\{x\in{\mathbb{R}}^n: Ax=b, x\geq 0\}.$$

Por el contrario, en el caso del método de puntos interiores el procedimiento consiste en aproximarse a la solución óptima a partir de un punto interior factible conocido, $x^0$. Ambos procedimientos se ilustran en la Figura (1.1).

Para hallar la solución óptima del problema (1.1) la dirección a seguir es aquella donde el valor de la función objetivo decrece. Este proceso debe ser repetido hasta alcanzar un punto interior suficientemente próximo a la solución óptima.

Específicamente uno tiene que responder las siguientes preguntas:

1. ¿Cómo empezar?, es decir, ¿cómo encontrar un punto interior factible inicial?.
2. ¿Cómo continuar?, es decir, conociendo un punto interior factible. ¿Cómo hacer para generar el siguiente punto que también sea interior factible y al mismo tiempo genere un menor valor en la función objetivo?.
3. ¿Cómo parar? Asumiendo que encontramos una respuesta satisfactoria para las dos preguntas anteriores. ¿Cuántas veces se formula la segunda pregunta?, ¿cuántos puntos se deberán generar?.