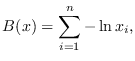Con la finalidad de mejorar el número de evaluaciones que realiza
el método Simplex para resolver un problema de programación
lineal, en 1984 Karmarkar propuso un método de puntos interiores
en el cual el número de evaluaciones para hallar el óptimo está
acotado por una función polinómica
[11],por lo tanto realiza menos evaluaciones que el método Simplex.
El método desarrollado por Karmarkar usa esferas y la proyección
geométrica para construir una sucesión de puntos interiores de la
región factible que convergen a la solución óptima generando así
un método de puntos interiores. La formulación del problema
de Programación Lineal que usa Karmarkar [9] es
donde
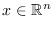 ,
,
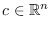 ,
,
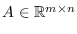 y
y
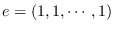 .
La validez del método de Karmarkar se basa en las siguientes condiciones:
.
La validez del método de Karmarkar se basa en las siguientes condiciones:
1.
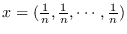 , satisface
, satisface 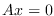 .
.
2. 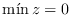 .
.
La restricción
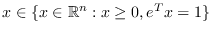 se reemplaza por
se reemplaza por 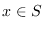 ,
donde
,
donde  es una esfera; simplificándose así el problema, pues el valor óptimo
se consigue aproximándose en forma iterada resolviendo un sistema de ecuaciones lineales.
es una esfera; simplificándose así el problema, pues el valor óptimo
se consigue aproximándose en forma iterada resolviendo un sistema de ecuaciones lineales.
A continuación se presenta un método de puntos interiores que
trabaja con el problema en su formulación estándar y no necesita
ningún conocimiento a priori del valor óptimo de la función
objetivo.
El cual es formulado de la siguiente manera:
mediante el método de puntos interiores: algoritmo del
elipsoide interior se inicia en un punto interior del poliedro
definido por las restricciones del problema lineal, el cual es
centro de un elipsoide incluido estrictamente en el poliedro. La
optimización de la función objetivo sobre el elipsoide,
proporciona un punto interior más próximo a la solución óptima.
Éste método genera una sucesión de puntos interiores que convergen
a la solución óptima del problema, para esto es necesario una
dirección de descenso, la cual se obtiene con la solución de un
problema de mínimos cuadrados en cada iteración.
El
problema de mínimos cuadrados, se resuelve por medio de la
equivalencia de calcular la proyección ortogonal de un vector
sobre el espacio nulo de una matriz que cambia en cada iteración y
para obtener una aproximación de esta matriz se construye un
método recursivo. Además garantizamos una “buena” aproximación
de esta matriz parametrizando la función objetivo mediante una
función llamada función barrera. En este caso usamos la función
barrera logarítmica [10] definida por:
el gradiente y el hessiano de esta función barrera involucra a la matriz que queremos aproximar.
Luego se usa la ecuación de la secante basada en la función
auxiliar con barrera logarítmica dada por:
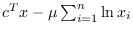 , y posteriormente se usa la fórmula
de actualización de Broyden para obtener una aproximación a la matriz.
Finalmente usando la fórmula de Sherman-Morrison-Woodburry
[14], se obtiene la aproximación a la dirección de
descenso; con esta dirección se obtiene un nuevo punto interior y
repitiendo este proceso en forma iterativa se obtiene una
aproximación a la solución óptima del Problema de programación
Lineal.
, y posteriormente se usa la fórmula
de actualización de Broyden para obtener una aproximación a la matriz.
Finalmente usando la fórmula de Sherman-Morrison-Woodburry
[14], se obtiene la aproximación a la dirección de
descenso; con esta dirección se obtiene un nuevo punto interior y
repitiendo este proceso en forma iterativa se obtiene una
aproximación a la solución óptima del Problema de programación
Lineal.
Utilizando estas herramientas y otras se construye un algoritmo
que permite resolver el problema lineal estándar, que a base de
teoremas la convergencia del método está garantizada.
Subsecciones