Siguiente: O Jogo do Baralho Subir: Compactificação de Informação via Anterior: Introducción
Um conjunto não-vazio,
![]() , é denominado espaço
métrico se existir uma função
, é denominado espaço
métrico se existir uma função
![]() , chamada métrica,
satisfazendo as seguintes condições:
, chamada métrica,
satisfazendo as seguintes condições:
(1)
![]() e
e
![]() se, e somente se,
se, e somente se,
![]() .
.
(2)
![]() .
.
(3)
![]() .
.
![]() denota o espaço métrico
denota o espaço métrico
![]() , munido da
métrica
, munido da
métrica ![]() .
.
Por exemplo, se para todo
![]() definimos
definimos
![]() , temos que
, temos que ![]() satisfaz as condições (1), (2) e (3)
acima, ou seja,
satisfaz as condições (1), (2) e (3)
acima, ou seja,
![]() é um espaço métrico. Esta
métrica é a métrica usual da reta real.
é um espaço métrico. Esta
métrica é a métrica usual da reta real.
Dizemos que um espaço métrico
![]() é discreto
se todo elemento
é discreto
se todo elemento
![]() é isolado, ou seja, quando
existe uma bola aberta em torno do ponto
é isolado, ou seja, quando
existe uma bola aberta em torno do ponto ![]() contendo unicamente o
próprio ponto
contendo unicamente o
próprio ponto ![]() . Se
. Se ![]() é uma métrica discreta, então o espaço
métrico
é uma métrica discreta, então o espaço
métrico
![]() é dito discreto. Por exemplo, o
conjunto dos inteiros
é dito discreto. Por exemplo, o
conjunto dos inteiros
![]() , com a métrica induzida da reta
real, é um espaço discreto.
, com a métrica induzida da reta
real, é um espaço discreto.
Dado
![]() um conjunto qualquer, sempre é
possível definir uma métrica
um conjunto qualquer, sempre é
possível definir uma métrica ![]() , chamada métrica
discreta, na forma:
, chamada métrica
discreta, na forma:
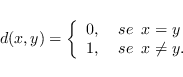
No espaço ![]() -dimensional
-dimensional
![]() , para
, para
![]() , definimos
, definimos
Por exemplo, em
![]() , temos
, temos
![]() .
.
No caso do corpo finito
![]() ,
para
,
para
![]() ,
definimos o peso de
Lee por
,
definimos o peso de
Lee por
![]() , onde
, onde
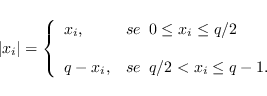
A distância de Lee entre
![]() é dada por
é dada por
![]() .
Verifica-se também que
.
Verifica-se também que ![]() é uma métrica.
é uma métrica.
Observação: A métrica de Hamming é utilizada em códigos
binários. Por outro lado, a métrica de Lee é utizada em códigos
provenientes de constelação de sinais ![]() , ou seja, quando os
sinais estão igualmente espaçados sobre um círculo. Caso a
constelação esteja sobre
, ou seja, quando os
sinais estão igualmente espaçados sobre um círculo. Caso a
constelação esteja sobre
![]() , o circulo em questão
é uma circunferência. Em ambos casos, o uso destas métricas
auxíliam a detecção e correção de possíveis erros que possam
ocorrer em uma transmissão de informação.
, o circulo em questão
é uma circunferência. Em ambos casos, o uso destas métricas
auxíliam a detecção e correção de possíveis erros que possam
ocorrer em uma transmissão de informação.